Pemahaman Mendalam tentang Sistem Bilangan

Sistem bilangan adalah konsep yang sangat penting dalam matematika. Ini adalah dasar dari pemahaman kita tentang angka dan operasi matematika. Dalam artikel ini, kita akan menjelaskan secara mendalam tentang sistem bilangan dan bagaimana sistem ini membentuk dasar dari seluruh bidang matematika.
1. Sistem Bilangan Desimal
Sistem bilangan yang paling umum digunakan di seluruh dunia adalah sistem bilangan desimal. Dalam sistem ini, kita memiliki sepuluh simbol dasar, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Posisi dari setiap angka dalam bilangan menunjukkan nilai tempatnya, mulai dari tempat satuan, puluhan, ratusan, dan seterusnya. Contohnya, dalam bilangan 356, angka 3 berada di posisi ratusan, angka 5 berada di posisi puluhan, dan angka 6 berada di posisi satuan.
2. Sistem Bilangan Lainnya
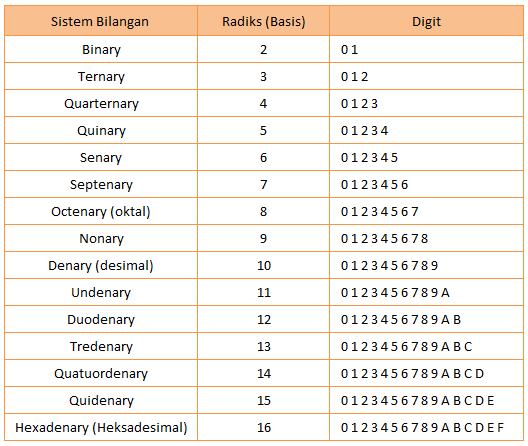
Selain sistem bilangan desimal, ada juga sistem bilangan lain yang digunakan dalam konteks khusus. Misalnya:
- Sistem Bilangan Biner (Binary): Digunakan dalam komputer, hanya terdiri dari angka 0 dan 1.
- Sistem Bilangan Oktal (Octal): Terdiri dari angka 0 hingga 7, digunakan dalam komputer dan pemrograman.
- Sistem Bilangan Heksadesimal (Hexadecimal): Terdiri dari angka 0-9 dan huruf A-F, juga digunakan dalam komputer.
Setiap sistem bilangan memiliki karakteristiknya sendiri dan digunakan dalam aplikasi yang berbeda-beda.
3. Operasi Matematika dalam Sistem Bilangan
Sistem bilangan memengaruhi bagaimana operasi matematika dilakukan. Dalam sistem bilangan desimal, operasi penjumlahan, pengurangan, perkalian, dan pembagian dilakukan sesuai dengan aturan tertentu. Namun, dalam sistem bilangan lain, seperti sistem biner, aturan ini berbeda.
4. Konsep Nol (0)
Konsep angka nol (0) adalah elemen penting dalam semua sistem bilangan. Angka nol adalah elemen identitas dalam operasi penjumlahan dan memiliki peran kritis dalam menentukan nilai tempat dalam sistem bilangan desimal. Tanpanya, kita akan kehilangan cara untuk menyusun angka-angka dengan benar dalam bilangan.
5. Penggunaan dalam Kehidupan Sehari-hari
Sistem bilangan digunakan dalam berbagai aspek kehidupan sehari-hari, mulai dari perhitungan keuangan, waktu, pengukuran, hingga ilmu pengetahuan dan teknologi. Tanpa pemahaman yang baik tentang sistem bilangan, banyak aspek kehidupan modern akan sulit untuk dijalankan.
6. Penerapan dalam Matematika Lanjutan
Sistem bilangan adalah dasar dari matematika lanjutan. Konsep ini berkembang menjadi teori bilangan, aljabar, analisis, dan cabang matematika lainnya. Dalam penelitian dan pengembangan ilmu pengetahuan, sistem bilangan juga memiliki peranan yang signifikan.
7. Kesimpulan
Pemahaman yang mendalam tentang sistem bilangan adalah kunci untuk memahami matematika dalam berbagai konteks. Ini adalah fondasi dari berbagai aspek matematika dan memiliki dampak yang luas dalam kehidupan sehari-hari serta penelitian ilmiah. Oleh karena itu, memahami sistem bilangan adalah langkah awal yang penting dalam memahami dunia matematika dengan lebih baik.


